We estimate our results over new data by using 5-fold cross validation [12]. Cross validation is the standard method to estimate likely predictions over unseen data in Data Mining. For each set of binary profiles we partitioned the data into 5 equal size groups. We used 4 of the partitions for training and then evaluated the rule set over the remaining partition. Then we repeated the process 5 times leaving out a different partition for testing each time. This gave us a very reliable measure of our method's accuracy over unseen data. We averaged the results of these five tests to obtain a good measure of how the algorithm performs over the entire set.
To evaluate our system we were interested in several quantities:
We were interested in the detection rate of the classifier. In our case this was the percentage of the total malicious programs labeled malicious. We were also interested in the false positive rate. This was the percentage of benign programs which were labeled as malicious, also called false alarms.
The Detection Rate is defined as
![]() ,
False Positive Rate as
,
False Positive Rate as
![]() ,
and Overall Accuracy as
,
and Overall Accuracy as
![]() .
The
results of all experiments are presented in Table 3.
.
The
results of all experiments are presented in Table 3.
|
For all the algorithms we plotted the detection rate vs. false positive rate using Receiver Operating Characteristic (ROC) curves [11]. ROC curves are a way of visualizing the trade-offs between detection and false positive rates.
As is shown in Table 3, the signature method had the lowest false positive rate, 0% This algorithm also had the lowest detection rate, 33.75%, and accuracy rate, 49.28%.
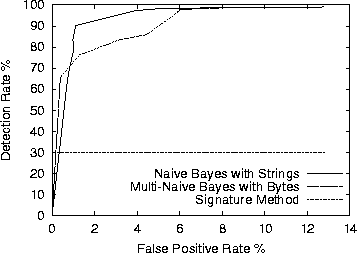
Since we use this method to compare with the learning algorithms we plot its ROC curves against the RIPPER algorithm in Figure 7 and against the Naive Bayes and Multi-Naive Bayes algorithms in Figure 8.
The detection rate of the signature-based method is inherently low over new executables because the signatures generated were never designed to detect new malicious executables. Also it should be noted that although the signature based method only detected 33.75% of new malicious programs, the method did detect 100% of the malicious binaries that it had seen before with a 0% false positive rate.
The RIPPER results shown in Table 3 are roughly equivalent to each other in detection rates and overall accuracy, but the method using features from Figure 2, a list of DLL function calls, has a higher detection rate.
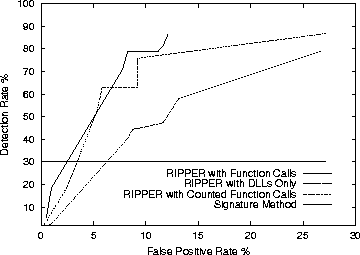 |
The ROC curves for all RIPPER variations are shown in Figure 7. The lowest line represents RIPPER using DLLs only as features, and it was roughly linear in its growth. This means that as we increase detection rate by 5% the false positive would also increase by roughly 5%.
The other lines are concave down so there was an optimal trade-off between detection and false alarms. For DLL's with Counted Function Calls this optimal point was when the false positive rate was 10% and the detection rate was equal to 75%. For DLLs with Function Calls the optimal point was when the false positive rate was 12% and the detection rate was less than 90%.
The Naive Bayes algorithm using strings as features performed the best out of the learning algorithms and better than the signature method in terms of false positive rate and overall accuracy (see Table 3). It is the most accurate algorithm with 97.11% and within 1% of the highest detection rate, Multi-Naive Bayes with 97.76%. It performed better than the RIPPER methods in every category.
In Figure 8, the slope of the Naive Bayes curve is initially much steeper than the Multi-Naive Bayes. The Naive Bayes with strings algorithm has better detection rates for small false positive rates. Its results were greater than 90% accuracy with a false positive rate less than 2%.
 |
The Multi-Naive Bayes algorithm using bytes as features had the highest detection
rate out of any method we tested, 97.76%. The false positive rate at 6.01% was
higher than the Naive Bayes methods (3.80%) and the signature methods (![]() ).
).
The ROC curves in Figure 8 show a slower growth than the Naive Bayes with strings method until the false positive rate climbed above 4%. Then the two algorithms converged for false positive rates greater than 6% with a detection rate greater than 95%.
The ROC curves in Figures 7 and 8 also let security experts understand how to tailor this framework to their specific needs. For example, in a secure computing setting, it may be more important to have a high detection rate of 98.79%, in which case the false positive rate would increase to 8.87%. Or if the framework were to be integrated into a mail server, it may be more important to have a low false positive rate below 1% (0.39% FP rate in our case) and a detection rate of 65.62% for new malicious programs.